Summary
I propose the index i, defined as the sum of the citations of a scientist’s top three single-authored works and the top three second-tier citations of each of those works, as a useful measure of a researcher’s innovativeness.
innovation | progress | advancement
Introduction
For the many scientists who follow the incentives of a scientific economic system, and “play the game not to lose,” their productivity is usually unquestionable. Among the rest of us, how does one quantify the impact of an individual’s impact on science? In a universe of virtually unlimited possible scientific discoveries, such quantification (even if potentially disruptive) is occasionally needed to show why that bucking the system contributes more to the advancement of science than blindly following the herd.
Hirsch (2005) invented h as the number of papers with citation number ≥ h. In the intervening years, h has been used for decisions on hiring, promotion, and grants. Unfortunately, this “herd” index has often meant culling exceptional types.
Indeed, h has been criticized on grounds that it fails to measure exceptional performance. Thus, some authors have proposed metrics that attempt to account more for high-impact works. Very often, it has been assumed that the deficiency of h is that it fails to distinguish between individuals with a similar h. Thus it has been assumed that if two scientists have an h = 50, possibly lurking between the two is one innovator and one imitator.
Most bibliometrics invented thus far have assumed that an innovator differs in degree and not kind from a producer. The approach thus has been to measure the typical parameters used to distinguish normal scientists from each other, under the assumption that an extended metric would distinguish an innovator. These can be divided into those that focus on number of papers in a researcher’s productive core (g and h(2)), or the impact of those papers (a or m) (Bornmann et al. 2008). g is the highest number g of papers that together received g2 citations. h(2) is the highest natural number such that a scientist’s h(2) most-cited papers received each at least h(2)2 citations (reviewed in Bornmann et al. 2008; their Table 1). To date, none of these alternative metrics have gained widespread use or are reported on Google Scholar pages.
Why have no other metrics succeeded? One reason is that other metrics are not really that different from h. A wolf is not just a gigantic sheep; it is qualitatively different. Statisticians have erred by applying the sheep’s metric to a wolf. You might, for example, classify a sheep based on how thick its coat of wool is. If you attempted to classify a wolf based on the thickness of its coat relative to a sheep, the wolf would not look superior at all (despite the sharp teeth, etc.). Statisticians have been fooled by what is normal for a flock of sheep. For example, they might see many scientists who publish tens or hundreds of papers in high-impact journals. They erroneously assume that it is necessary to allow for tens or hundreds of papers to gauge an innovator’s “productive core.”
In reality, the wolves of science are simple creatures. They do not have to write tens or hundreds of papers to appear innovative. Instead, they have one or two new ideas and devote their lives to developing and disseminating those ideas. Former metrics that attempted to measure innovativeness confused a wolf with sheep in wolf’s clothing.
Here, I propose i as a metric of scientific innovativeness. My primary assumption is that any individual scientist’s impact can be distinguished by the quality of only three single-authored articles and the articles that cite those. This core assumption is so powerful that a couple of other apparently unrealistic assumptions do not impact the results.
To evaluate i, I ask whether it adequately classifies scientists in biology according to their innovativeness, as judged by the independent metric of Nobel-equivalent prizes (i.e., Craaford and Kyoto prizes; for a field in which Nobels are not awarded) and my own subjective knowledge of the field.
Methods
I calculated i as the sum of the citations of a scientist’s top three single-authored works and the top three second-tier citations of each of those works (Fig. 1). On May 30, 2018, I calculated i for 44 evolutionary biologists whose work I am familiar with. I also included a couple of molecular biologists with top h‘s cited by Hirsch (2005).
Figure 1. Example of i calculation. Darwin’s i score is calculated as the sum of all the numbers in parentheses. An attractive quality of i is that it can be calculated quickly.
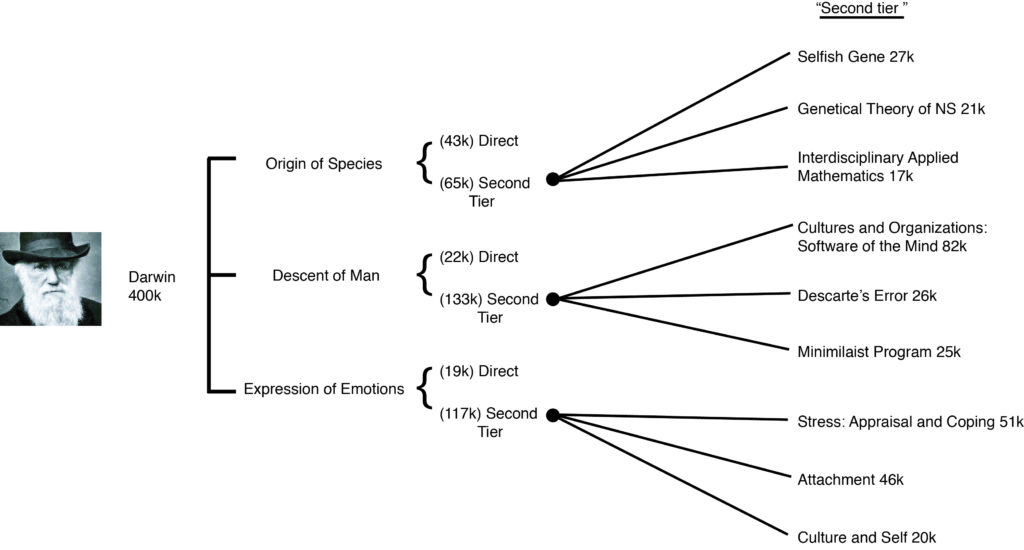
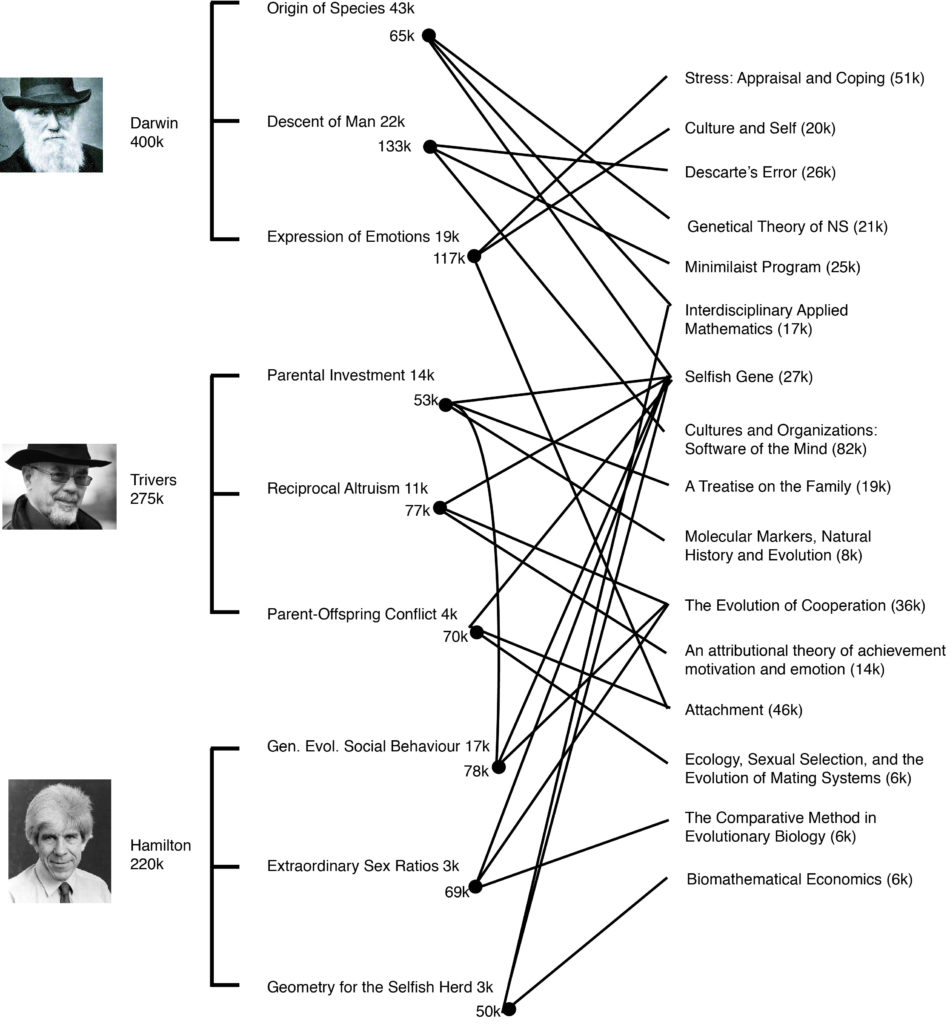
Figure 2. The top three biologists whose i was determined by theoretical works (in the sample).
Results
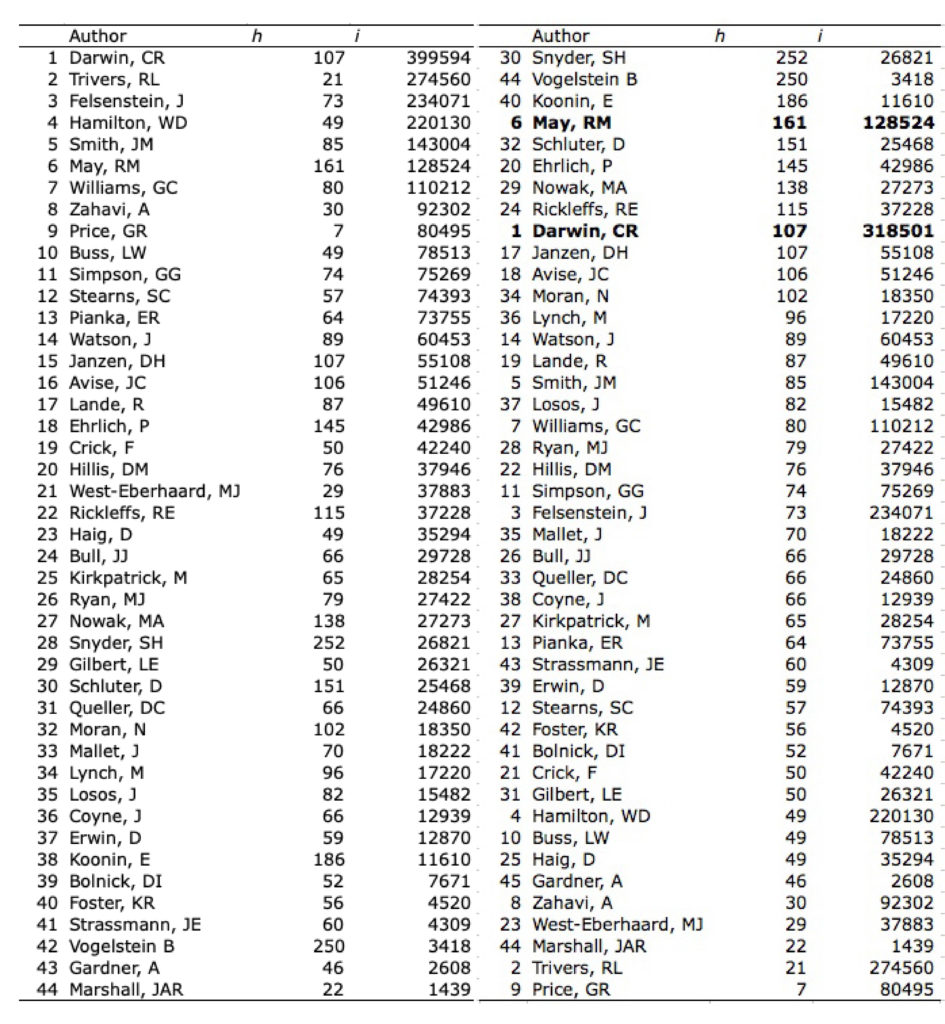
The first result is i categorizes people well according to innovativeness. In the top 10 of i were Darwin, Trivers, Felsenstein, Hamilton, Maynard Smith, May, Williams, Zahavi, Price, and Buss (Fig. 3 photos). This agrees with my subjective knowledge of the field. Also agreeing was that there were 6 Nobel-type prizes awarded to the top ten of i compared to only 3 for the top ten of h (Trivers [Craaford], Hamilton [both], Maynard Smith [both], Williams [Craaford] in the top i vs. Ehrlic [Craaford] and Janzen [both] in the top h). The top i had double the number of prizes, even though their h was less than half as large on average (66.2 ± 14.4 s.e. vs. 161.2 ± 16.9 s.e.).
Figure 3. Scatterplot of h and i. There is no correlation between h and i (r square = 0.02, p = 0.36; N= 44).
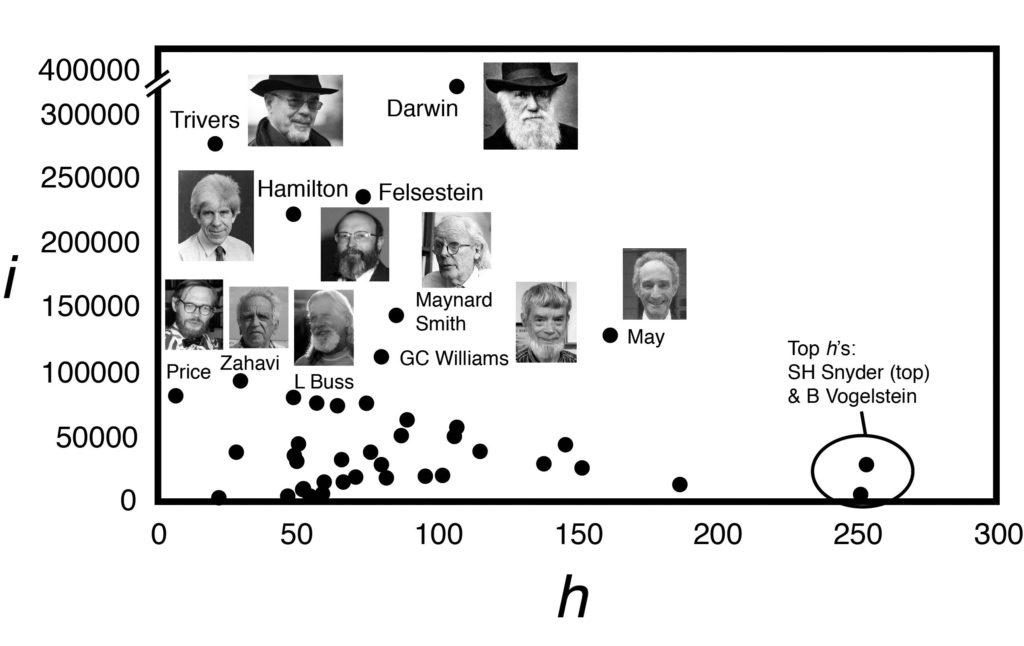
Although i categorized people according to their innovativeness, there is no overall correlation between i and h (r square = 0.02, p = 0.36; N= 44). People with high h did not necessarily have high i, and vice versa. For example, W. D. Hamilton, Leo Buss, Amotz Zahavi, Robert Trivers and George Price all were in the top 10 of i and bottom 10 of h. B Vogelstein who had the second-highest h (h = 250) had the third lowest i (i = 3418).
Charles Darwin and Robert May are the only two individuals who made the top-10 lists of both h and i in this sample. Darwin was the more innovative as measured by i, while May was more prolific as measured by h. Robert Trivers had the second highest i (i = 274k) despite having the second-lowest h (h = 21).
In his original paper on h, Hirsch (2005) argued that, “…two individuals with similar hs are comparable in terms of their overall scientific impact, even if…their total number of citations is very different.” The i factor refutes this statement. W. D. Hamilton (b. 1936), Leo Buss (b. 1953), and David Haig (b. 1958) all had the same h = 49, but very different i scores (Haig, 35k; Buss, 79k; Hamilton, 220k, respectively). This suggests individuals with different h are not comparable in their overall scientific impact.
Table 1. Results. Sample sorted by i (left) and h (right).
One of the implicit assumptions of the i index is that the simplest measure, which sums the first (direct) and second tier citations, suffices to yield a metric of innovativeness. This assumption might hold because specialized works, like Hamilton’s Sex Ratios, and general works like Darwin’s Origin, both receive second tier citations (Fig. 2). However, only general works tend to have a high percent first tier citations (Table 2). Weighting second tier citations in this way allows more specialized works to have a similar impact as general works. This is warranted because specialized works can have major impacts on a field on par with those of general works (e.g., Trivers’ Parent-Offspring Conflict had a similar as Parental Investment, despite the large discrepancy in percent first tier citations; Fig. 2 and Table 2). Similarly, Hamilton’s Sex Ratios paper had a large impact that would have been ignored if second tier citations were not sufficiently weighted.
Table 2. Ideas and percent first tier for the i-scoring papers of Darwin, Trivers, and Hamilton. Percent first tier is the percent of the i–contributing score of a paper derived from 1st tier citations. For Darwin’s Origin, for example, percent first tier is calculated as 43 / (43 + 65) (see Fig. 2).

I also assumed that it is possible to gauge a scientist’ innovativeness without paying attention to whether second tier works are “scientific” or if they are ever counted multiple times. For example, Robert Trivers’ top three highly-cited works are Parental Investment, Reciprocal Altruism, and Parent-Offspring Conflict. Each was cited by The Selfish Gene. By including The Selfish Gene as a second-tier citation for both, The Selfish Gene was counted thrice toward Trivers’ i. This certainly influenced the results, but was it warranted? I argue that it is for a couple of reasons. First, The Selfish Gene was one of the most important scientific works of the 20th century for disseminating important ideas (e.g., The Selfish Gene contributed 21% of the i scores of Darwin, Trivers, and Hamilton combined; see also Fig. 2). Second, if three different people had written Trivers’ top three papers, then each person would have been justified for being credited with the second-tier citations from The Selfish Gene. Thus it makes sense that Trivers was credited three times.
Discussion
The i factor thus succeeds as a measure of scientific innovativeness despite its absurd simplicity. But what exactly is meant by innovativeness? According to Gilbert (2019), innovativeness consists of inventiveness (creating or originating) and entrepreneurship (disseminating). The data suggest that one can achieve a high i score by either being entrepreneurial, or by being a combination of inventive and entrepreneurial.
What are some specific examples of inventiveness and entrepreneurship among individuals in the top 10 of i? An example of an individual who achieved a high i through pure entrepreneurship is John Maynard Smith (i =143k). Maynard Smith’s i score was derived from developing and disseminating Price’s idea of game theory and Hamilton’s idea of nepotism. Maynard Smith did not come up with the ideas himself. He achieved his i with his paper The theory of games and the evolution of animal conflicts (78k), his book Evolution and The Theory of Games (58k), and his paper Group selection and kin selection (43k). Maynard Smith’s talent was not in coming up with ideas, but in recognizing important ideas, developing them in unique ways, and disseminating them to large audiences.
In contrast, most other authors on the top ten list of i are better classified as hybrid inventor-entrepreneurs because they played a role in both originating and disseminating their ideas. Trivers, May, Williams, Zahavi, Price, and Buss were all highly imaginative and creative, as well as effective disseminators. Felsenstein derived his large i score from methodological papers, and probably had to employ a fair degree of both inventiveness and entrepreneurship. There are no examples of people with high i scores who created but did not disseminate ideas. This would be like a Coca Cola company that does not ship or market its product.
What positive impact might i have on science? One benefit of adopting i would be that scientists would have more of a choice early in their career to choose whether to produce or innovate. As it is currently, the mantra is, “publish or perish,” which is essentially “produce or perish.” In a climate where i is adopted as a metric, scientists might have more incentive to innovate. To use a Gouldian baseball analogy, the situation is reminiscent of the early days of baseball, when batting average (the percentage of at bats that results in the runner on base) was taken to be the primary statistic relevant to hitting. Baseball players were often hired or given raises based on their batting averages. The consequence was that players were incentivized to increase their batting averages, at the cost of big hits with many runners on base, or getting on base by walking. Introduction of new statistics like slugging percentage, runs batted in, and on base percentage, incentivized baseball players to become better hitters and smarter players. Including additional metrics like i might incentivize scientists to do more innovative research.
What barriers might stand in the way of adoption of i? One is that university administrators with short-term horizons are incentivized to favor immediate monetary gains at the cost of genuine scientific advances. Administrators will thus favor h because it is biased toward costly research (research involving large teams, experiments, and expensive equipment). Another is that professors, anticipating the administrator’s responses, themselves favor candidates who they think will “succeed” under such pressures (not because they necessarily agree with them). Professors have not yet taken a unified stance against administrators—though perhaps i will help them think about why they should. Finally, scientists with high hs and low is, who are accustomed to being the top of the herd, have an automatic bias against i. Problematically, those who innovate must understand the importance of normal science, but those who have never innovated need not understand the importance of what Kuhn calls “revolutionary science” or what history books call “science.”
On the bright side, however, i shows that it is never too late to become a scientific innovator. All you need is one good idea. All of Darwin’s works contributing to his i were based on natural selection. All of Price’s works were based on covariance mathematics applied to selection. All of Zahavi’s works were based on the handicap principle. Moreover, if you can’t come up with a single idea yourself (most people can’t), all you have to do is steal a good idea (disclaimer: I am not recommending you take an idea without citing the source. Instead, you will get more credit if you “steal in plain sight,” heaping credit on the originator and developing it yourself. This why Maynard Smith is known as the father of evolutionary game theory, even though he said himself, “if there is anything in the idea, the credit should go to Dr. Price and not to me;” see Maynard Smith 1972, p. viii).
In conclusion, i classifies biologists according to their innovativeness. In contrast to other metrics that attempt to measure exceptional performance, i focuses on a few key articles and allows for the impact of articles that cite them. The lack of observed correlation between i and h suggests h is severely lacking as metric of scientific impact. It also suggest that the current situation of science, in which fields are dominated by large task forces of specialists doing incremental research designed for costliness, is in part dependent upon employment of h as a metric for career and grant evaluation. Including i, or something like it, as a metric may help improve science as an engine of innovation and progress.
Acknowledgments
I thank Tom Gilbert for suggesting the comparison between the current situation in science and the former situation in baseball.
Literature Cited
Bornmann et al. 2008 Are there better indices for evaluation purposes than the h index? a comparison of nine different variants of the h index using data from biomedicine. J Amer Soc Info Sci Tech. 59(5):830-837.
Gilbert, Owen M. 2019. Natural reward as the fundamental macroevolutionary force. arXiv preprint arXiv:1903.09567.
Hirsch, J. E. 2005. An index to quantify an individual’s scientific research output. Proc Nat. Acad Sci USA 102(46):16569-16572.
Maynard Smith, J. 1972. On Evolution. Edinburgh University Press. Edinburgh, UK.